Vous vous demandez comment doubler votre capital en 1 an ou comment investir efficacement ? L’astuce réside dans la maîtrise du calcul des intérêts composés. À travers cet article, nous vous aidons à comprendre le fonctionnement et la formule des intérêts composés, avec des exemples concrets.
Définition des intérêts composés
Les intérêts composés, aussi appelés intérêts capitalisés ou intérêts cumulés, représentent la rémunération obtenue lorsque les intérêts générés sur un capital sont réinvestis pour produire à leur tour des intérêts. Ce mécanisme, qualifié de “8e merveille du monde” par Albert Einstein, permet d’augmenter progressivement le capital et ainsi maximiser le rendement sur le long terme.
C’est un principe de base en finance qui illustre le potentiel de croissance de l’argent placé ou investi, où les intérêts générés sont constamment réinvestis, créant un effet de “boule de neige”. Ainsi, les intérêts composés ne se limitent pas à rapporter sur le capital initial, mais également sur les intérêts accumulés précédemment.
Par exemple, si vous placez une somme d’argent à un certain taux d’intérêt, non seulement cette somme initiale va générer des intérêts, mais ces intérêts vont à leur tour produire des intérêts. C’est ce qu’on appelle l’effet des intérêts composés.
En bref, les intérêts composés sont une technique de capitalisation qui permet d’accroître significativement le rendement d’un investissement sur le long terme.
Principe de fonctionnement des intérêts composés
Le fonctionnement des intérêts composés repose sur 2 éléments clés : le réinvestissement des intérêts et le temps.
Dans le cadre des intérêts composés, les intérêts générés par votre capital ne sont pas simplement versés sur votre compte, ils sont réinvestis. Cela signifie que ces intérêts vont eux-mêmes produire des intérêts lors de la prochaine période de capitalisation. On parle alors d'”intérêts sur les intérêts”.
Le temps joue un rôle crucial dans ce processus. Plus vous laissez votre argent investi, plus l’effet des intérêts composés sera puissant. En effet, chaque période de capitalisation permet d’ajouter les intérêts générés au capital initial, augmentant ainsi la base de calcul des intérêts pour la période suivante.
Ainsi, le principe des intérêts composés peut se résumer par la phrase suivante : “L’argent produit de l’argent qui produit de l’argent et ainsi de suite”. Il s’agit donc d’un mécanisme d’accumulation exponentielle du capital, favorisant une croissance rapide de votre investissement sur le long terme.
Comment calculer les intérêts cumulés : formule et tableau
Pour calculer les intérêts composés, vous pouvez utiliser la formule suivante :
Cn = Co(1+i)^n
- Cn est le capital final après n périodes,
- Co est le capital initial,
- i est le taux d’intérêt par période,
- n est le nombre de périodes.
Pour bien visualiser l’accumulation des intérêts, il peut être intéressant de construire un tableau de capitalisation. Par exemple, si vous voulez suivre l’évolution d’un placement sur 5 ans avec un taux d’intérêt annuel de 4%, vous pouvez organiser votre tableau de cette manière :
| wdt_ID | Année | Capital de départ | Intérêts de l'année | Capital de fin d'année |
|---|---|---|---|---|
| 1 | 1 | Co | Co*i | Co*(1+i) |
| 2 | 2 | Co*(1+i) | Co*(1+i)*i | Co*(1+i)^2 |
| 3 | 3 | Co*(1+i)^2 | Co*(1+i)^2*i | Co*(1+i)^3 |
| 4 | 4 | Co*(1+i)^3 | Co*(1+i)^3*i | Co*(1+i)^4 |
| 5 | 5 | Co*(1+i)^4 | Co*(1+i)^4*i | Co*(1+i)^5 |
Ainsi, vous pourrez observer l’effet des intérêts composés sur votre capital initial.
Exemple d’application du calcul des intérêts composés
Pour illustrer l’application du calcul des intérêts composés, prenons un exemple concret.
👉 Supposons que vous disposez d’un capital initial de 1000 euros que vous placez sur une assurance vie avec un taux d’intérêt annuel de 5%. Les intérêts sont composés annuellement, c’est-à-dire que chaque année, les intérêts générés sont ajoutés au capital initial pour le calcul des intérêts de l’année suivante.
- Après la première année, vous obtenez des intérêts de 1000 * 5% = 50 euros. Votre capital devient donc 1000 + 50 = 1050 euros.
- Lors de la deuxième année, les intérêts sont calculés sur la nouvelle somme de 1050 euros. Ainsi, vous obtenez des intérêts de 1050 * 5% = 52,5 euros. Votre capital devient alors 1050 + 52,5 = 1102,5 euros.
- Le processus continue pour les années suivantes.
Cet exemple montre clairement l’effet de l’accumulation des intérêts sur le capital. Plus le temps passe, plus les intérêts générés sont élevés, ce qui accélère la rentabilité de votre capital.
Intérêts composés vs intérêts simples : une comparaison
Au-delà de la définition, il est essentiel de comprendre la différence entre intérêts composés et intérêts simples pour faire de bons choix d’investissement. Les intérêts simples se basent uniquement sur le capital initial, sans tenir compte des intérêts précédemment acquis.
👉 Par conséquent, si vous placez 1000 € pendant 5 ans à un taux d’intérêt de 5% en intérêts simples, vous gagnerez chaque année 50 €, soit un total de 250 € après 5 ans.
En revanche, avec les intérêts composés, les intérêts générés sont réinvestis et génèrent à leur tour des intérêts.
👉 Dans le même exemple, avec un taux d’intérêt de 5% composé annuellement, votre investissement de 1000 € aurait généré plus de 276 € d’intérêts après 5 ans. Ce qui démontre clairement la puissance des intérêts composés par rapport aux intérêts simples.
Mais, retenez que l’effet des intérêts composés est d’autant plus significatif sur le long terme.
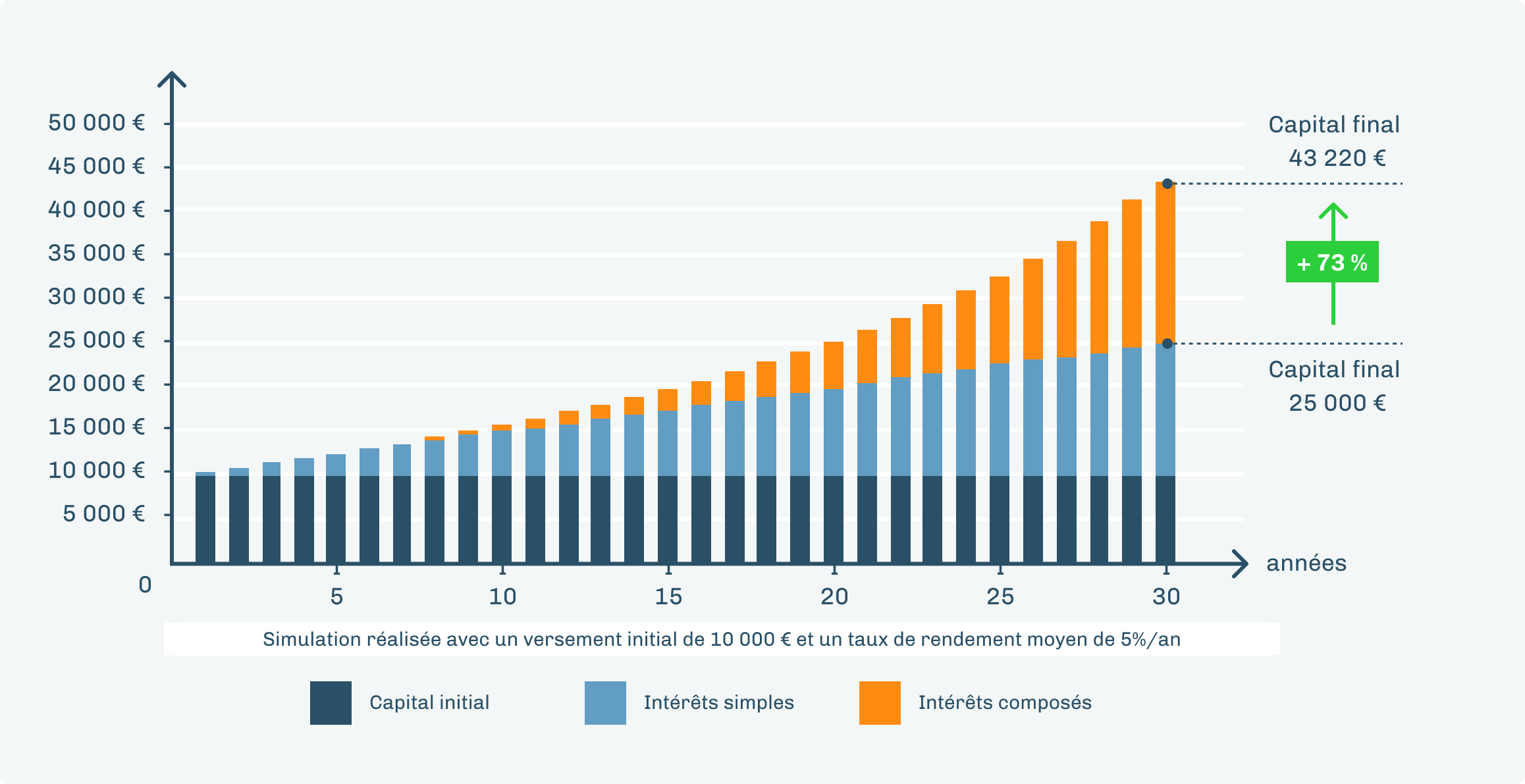
Les intérêts composés dans le domaine de l’investissement
En investissement, les intérêts composés sont considérés comme un puissant levier de croissance. En effet, ils permettent d’augmenter la valeur de votre investissement de façon exponentielle, surtout sur le long terme. Ils sont donc particulièrement intéressants pour les investisseurs ayant une stratégie d’investissement à long terme.
Les intérêts composés s’appliquent à divers types de placements : livrets d’épargne, assurance vie, PER, bourse…
Comment fonctionnent les intérêts composés en bourse ?
Lorsque vous achetez des actions, les dividendes que vous recevez peuvent être réinvestis pour acheter d’autres actions. Chaque réinvestissement de dividendes augmente le nombre d’actions détenues. Ainsi, les dividendes futurs sont calculés sur une base de capital plus importante, ce qui conduit à des gains plus élevés. Ce mécanisme de réinvestissement des dividendes est l’application des intérêts composés en bourse.
Les intérêts peuvent être composés à différentes fréquences : annuelle, semestrielle, trimestrielle, mensuelle, ou même de manière continue. Plus la fréquence de composition est élevée, plus la performance de l’investissement sera importante.
La patience est un facteur clé pour maximiser les bénéfices des intérêts composés en bourse. Plus le capital reste investi, plus les intérêts composés ont le temps de travailler et d’augmenter la valeur de l’investissement.
Où placer son argent pour avoir des intérêts composés ?
Pour bénéficier des intérêts composés, vous pouvez vous orienter vers plusieurs produits :
- Les livrets d’épargne réglementés comme le Livret A ou le Livret de Développement Durable et Solidaire (LDDS) sont des choix sans risque qui produisent des intérêts chaque année.
- Les assurances vie et les PER sont également un choix judicieux, notamment pour leur flexibilité et leur potentiel de rendement.
- L’investissement en bourse, grâce au réinvestissement des dividendes, permet d’exploiter pleinement la puissance des intérêts composés.
Les ETFs et les intérêts composés : un duo gagnant ?
L’association d’ETFs (Exchange Traded Funds) et des intérêts composés peut être une stratégie d’investissement efficace. Les ETFs, aussi appelés trackers, sont des fonds de placement qui reproduisent la performance d’un indice boursier. Ils permettent ainsi une diversification instantanée de votre portefeuille.
Quant aux intérêts composés, ils augmentent la valeur de votre investissement de façon exponentielle. Le réinvestissement des dividendes perçus grâce aux ETFs permet de bénéficier de ce phénomène.
En pratique :
- Vous achetez des parts d’ETF, qui génèrent des dividendes.
- Ces dividendes sont automatiquement réinvestis pour acheter d’autres parts d’ETF.
- Cela accroît le nombre de vos parts, et par conséquent, vos futurs dividendes.
Cette stratégie, dite de capitalisation, fait travailler votre argent en continu et maximise l’effet des intérêts composés. C’est donc une méthode qui peut être profitable sur le long terme.
Comment doubler son capital en 1 an grâce aux intérêts composés ?
Pour doubler son capital, une méthode couramment utilisée est la règle de 72. La règle de 72 est une formule simple pour estimer le temps nécessaire pour doubler un investissement grâce aux intérêts composés. Il suffit de diviser 72 par le taux d’intérêt annuel. Par exemple, si vous avez un taux d’intérêt de 6%, cela prendrait environ 12 ans (72/6) pour doubler votre capital. Un taux d’intérêt de 12% doublerait votre capital en 6 ans.
Cependant, pour atteindre cet objectif en un an, il faudrait un taux d’intérêt exceptionnellement élevé. En effet, selon la règle de 72, vous auriez besoin d’un taux d’intérêt mensuel de 6% pour doubler votre investissement en un an…
Comment investir dans les intérêts composés ? L’association des versements programmés
Pour tirer le meilleur parti des intérêts composés, l’association avec les versements programmés est une stratégie efficace. Cette méthode consiste à investir une somme fixe à des intervalles réguliers (mensuels, trimestriels, etc.), indépendamment des fluctuations du marché.
Cette technique, aussi appelée “dollar-cost averaging” (DCA), permet de réduire le risque lié à la volatilité des marchés en achetant plus d’actifs lorsque les prix sont bas et moins lorsque les prix sont élevés.
Avec les versements programmés, vos gains sont réinvestis, ce qui augmente votre capital de manière exponentielle grâce à l’effet des intérêts composés. Ainsi, votre capital initial et les versements réguliers profitent de l’effet de capitalisation sur le long terme.





